Understanding Memory Formats¶
Introduction¶
Most computations are about data: analyzing data, adjusting data, reading and storing data, generating data, etc. The DNN domain is no exception. Images, weights/filters, sound, and text require efficient representation in computer memory to facilitate performing operations fast and in the most convenient way.
This article is devoted to data format one form of data representation that describes how multidimensional arrays (nD) are stored in linear (1D) memory address space and why this is important for oneDNN.
Note
For the purpose of this article, data format and layout are used interchangeably.
Nomenclature used¶
Channels are the same as feature maps
Upper-case letters denote the dimensions (e.g.
N)Lower-case letters denote the index (e.g.
n, where0 <= n < N)The notation for the activations:
batch N, channels C, depth D, height H, width W
The notation for the weights:
groups G, output channels O, input channels I, depth D, height H, width W
Data formats¶
Let’s first focus on data formats for activations (images).
Activations consist of channels (also called feature maps) and a spatial domain, 1D, 2D, or 3D. The spatial domain together with channels form an image. During the training phase, images are typically grouped together in batches. Even if there is only one image, we still assume that there is a batch with batch size equal to 1. Hence, the overall dimensionality of activations is 4D (N, C, H, and W) or 5D (N, C, D, H, and W).
For the sake of simplicity, we will use only 2D spatial in this article.
Plain data formats¶
It would be simpler to start with an example.
Consider 4D activations with batch equals 2, 16 channels, and 5 x 4 spatial domain. Logical representation is given in the picture below.
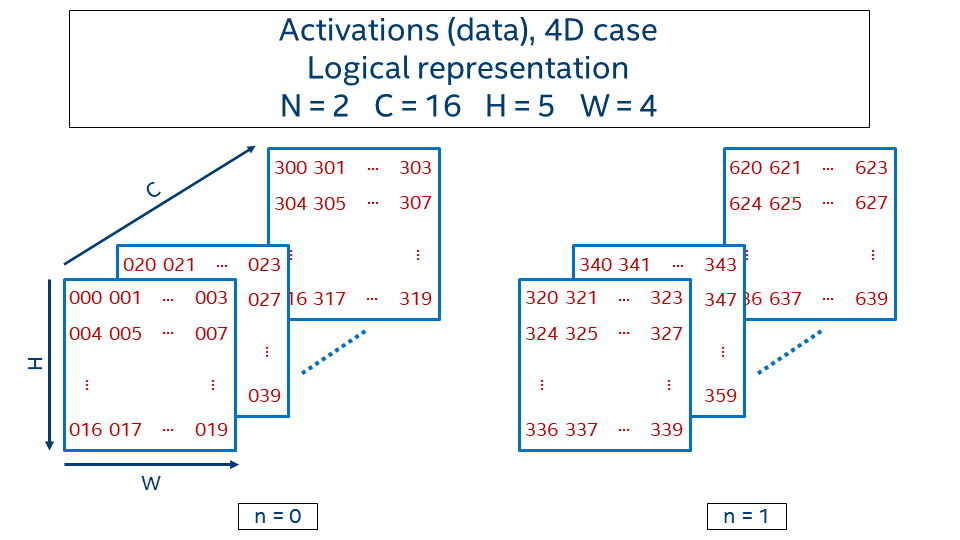
The value at the position (n, c, h, w) is generated with the following formula:
value(n, c, h, w) = n * CHW + c * HW + h * W + w
In order to define how data in this 4D-tensor is laid out in memory, we need to define how to map it to a 1D tensor via an offset function that takes a logical index (n, c, h, w) as an input and returns an address displacement to the location of the value:
offset : (int, int, int, int) --> int
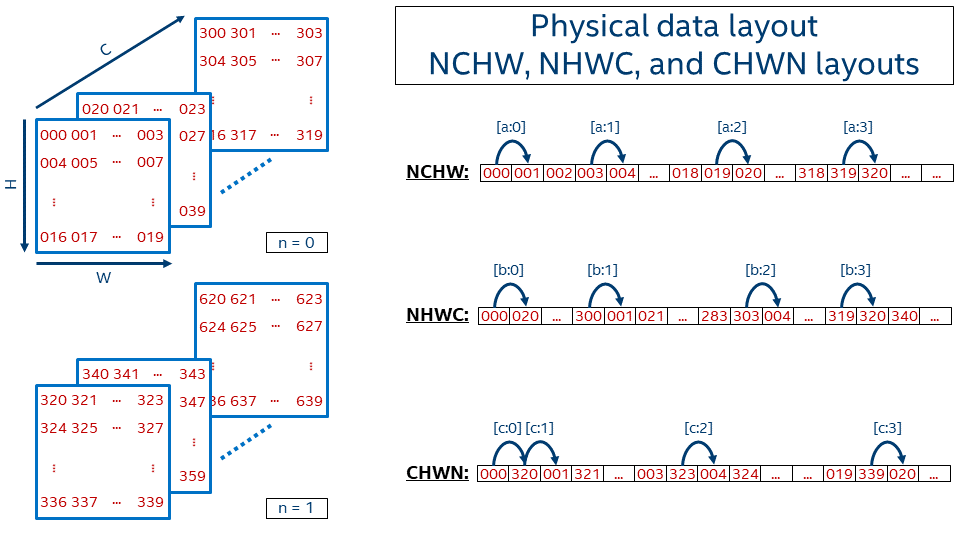
NCHW¶
Let’s describe the order in which the tensor values are laid out in memory for one of the very popular formats, NCHW. The [a:?] marks refer to the jumps shown in the picture below, which shows the 1D representation of an NCHW tensor in memory.
[a:0]First within a line, from left to right[a:1]Then line by line from top to bottom[a:2]Then go from one plane to another (in depth)[a:3]And finally switch from one image in a batch (n = 0) to another (n = 1)
Then the offset function is:
offset_nchw(n, c, h, w) = n * CHW + c * HW + h * W + w
We use nchw here to denote that w is the inner-most dimension, meaning that two elements adjacent in memory would share the same indices of n, c, and h, and their index of w would be different by 1. This is of course true only for non-border elements. On the contrary, n is the outermost dimension here, meaning that if you need to take the same pixel (c, h, w) but on the next image, you have to jump over the whole image size C*H*W.
This data format is called NCHW and is used by default in BVLC* Caffe. TensorFlow* also supports this data format.
Note
It is just a coincidence that offset_nchw() is the same as value() in this example.
One can create memory with NCHW data layout using dnnl_nchw of the enum type dnnl_format_tag_t defined in dnnl_types.h for the C API, and dnnl::memory::format_tag::nchw defined in dnnl.hpp for the C++ API.
NHWC¶
Another quite popular data format is NHWC, which uses the following offset function:
offset_nhwc(n, c, h, w) = n * HWC + h * WC + w * C + c
In this case, the inner-most dimension is channels ([b:0]), which is followed by width ([b:1]), height ([b:2]), and finally batch ([b:3]).
For a single image (N = 1), this format is very similar to how BMP-file format works, where the image is kept pixel by pixel and every pixel contains all required information about colors (for instance, three channels for 24bit BMP).
NHWC data format is the default one for TensorFlow.
This layout corresponds to dnnl_nhwc or dnnl::memory::format_tag::nhwc.
CHWN¶
The last example here for the plain data layout is CHWN, which is used by Neon. This layout might be very interesting from a vectorization perspective if an appropriate batch size is used, but on the other hand users cannot always have good batch size (for example, in case of real-time inference batch is typically 1).
The dimensions order is (from inner-most to outer-most): batch ([c:0]), width ([c:1]), height ([c:2]), channels ([c:3]).
The offset function for CHWN format is defined as:
offset_chwn(n, c, h, w) = c * HWN + h * WN + w * N + n
This layout corresponds to dnnl_chwn or dnnl::memory::format_tag::chwn.
Relevant reading¶
Generalization of the plain data layout¶
Strides¶
In the previous examples the data was kept packed or in dense form, meaning pixels follow one another. Sometimes it might be necessary to not keep data contiguous in memory. For instance, some might need to work with a sub-tensor within a bigger tensor. Sometimes it might be beneficial to artificially make the data disjoint, as in case of GEMM with a non-trivial leading dimension to get better performance (see Tips 6).
The following picture shows a simplified case for a 2D matrix of size rows x columns kept in row-major format where rows have some non-trivial (that is, not equal to the number of columns) stride.
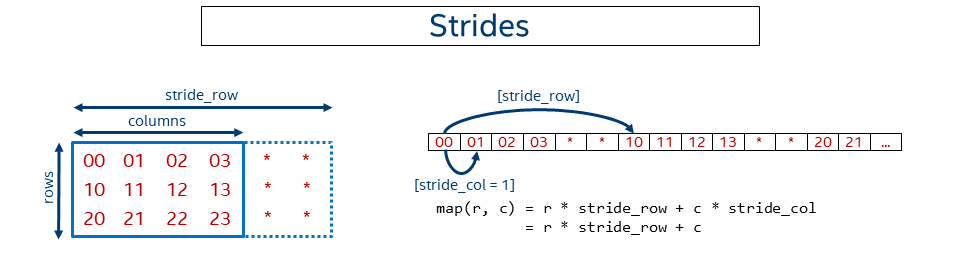
In this case, the general offset function looks like:
offset(n, c, h, w) = n * stride_n + c * stride_c + h * stride_h + w * stride_w
Note that the NCHW, NHWC, and CHWN formats are just special cases of the format with strides. For example, for NCHW we have:
stride_n = CHW, stride_c = HW, stride_h = W, stride_w = 1
A user can initialize a memory descriptor with strides:
dnnl_dims_t dims = {N, C, H, W}; dnnl_dims_t strides = {stride_n, stride_c, stride_h, stride_w}; dnnl_memory_desc_t md; dnnl_memory_desc_init_by_strides(&md, 4, dims, dnnl_f32, strides);
oneDNN supports strides via blocking structure. The pseudo-code for the function above is:
memory_desc_t md; // memory descriptor object // logical description, layout independent md.ndims = 4; // # dimensions md.dims = {N, C, H, W}; // dimensions themselves // physical description md.format_kind = dnnl_blocked; // generic blocked format md.format_desc.blocking.strides = { stride_n, stride_c, stride_h, stride_w };
In particular, whenever a user creates memory with the dnnl_nchw format, oneDNN computes the strides and fills the structure on behalf of the user.
Blocked layout¶
Plain layouts give great flexibility and are very convenient for use. That’s why most of the frameworks and applications use either the NCHW or NHWC layout. However, depending on the operation that is performed on data, it might turn out that those layouts are sub-optimal from the performance perspective.
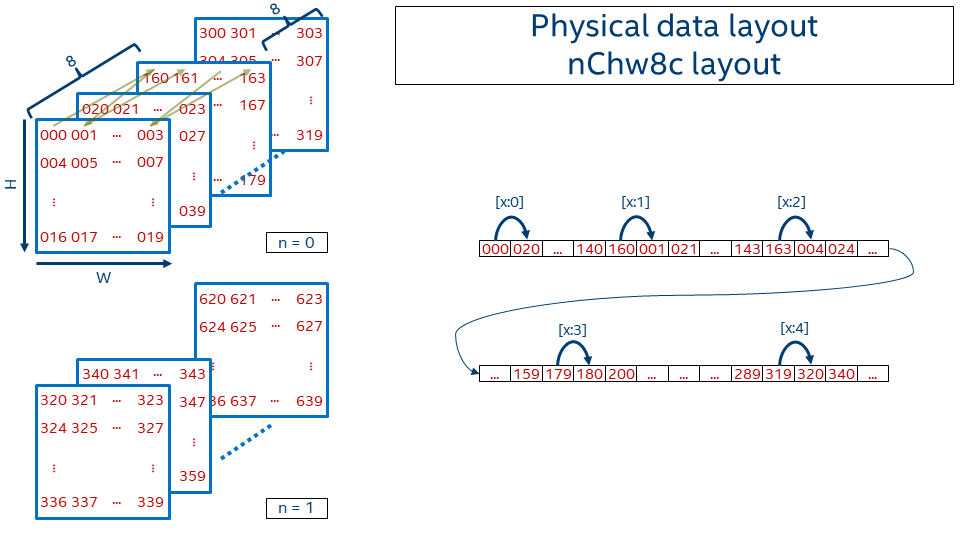
In order to achieve better vectorization and cache reuse oneDNN introduces blocked layout that splits one or several dimensions into the blocks of fixed size. The most popular oneDNN data format is nChw16c on AVX512+ systems and nChw8c on SSE4.1+ systems. As one might guess from the name the only dimension that is blocked is channels and the block size is either 16 in the former case or 8 in the later case.
Precisely, the offset function for nChw8c is:
offset_nChw8c(n, c, h, w) = n * CHW + (c / 8) * HW*8 + h * W*8 + w * 8 + (c % 8)
Note that blocks of 8 channels are kept contiguously in memory. Pixel by pixel the spatial domain is covered. Then next slice covers the subsequent 8 channels (that is, moving from c=0..7 to c=8..15). Once all channel blocks are covered, the next image in the batch appears.
Note
We use lower- and uppercase letters in the formats to distinguish between the blocks (e.g. 8c) and the remaining co-dimension (C = channels / 8).
The reason behind the format choice can be found in this paper.
oneDNN describes this type of memory via blocking structure as well. The pseudo-code is:
memory_desc_t md; // logical description, layout independent md.ndims = 4; // # dimensions md.dims = {N, C, H, W}; // dimensions themselves // physical description md.memory_format = dnnl_blocked; // blocked layout ptrdiff_t stride_n = C*H*W; ptrdiff_t stride_C = H*W*8; ptrdiff_t stride_h = W*8; ptrdiff_t stride_w = 8; md.format_desc.blocking.strides = { // strides between blocks stride_n, stride_C, stride_h, stride_w }; md.format_desc.inner_nblks = 1; // number of blocked dimensions; // 1, since only channels are blocked md.format_desc.inner_idxs[0] = 1; // Only the 1st (c) dimension is blocked // n -- 0st dim, w -- 3rd dim md.format_desc.inner_blks[0] = 8; // This 1st dimensions is blocked by 8
What if channels are not a multiple of 8 (or 16)?¶
The blocking data layout gives a significant performance improvement for the convolutions, but what to do when the number of channels is not a multiple of the block size (for example, 17 channels for nChw8c format)?
One of the possible ways to handle that would be to use blocked layout for as many channels as possible by rounding them down to a number that is a multiple of the block size (in this case 16 = 17 / 8 * 8) and process the tail somehow. However, that would lead to the introduction of very special tail-processing code into many oneDNN kernels.
So we came up with another solution using zero-padding. The idea is to round the channels up to make them multiples of the block size and pad the resulting tail with zeros (in the example above, 24 = div_up(17, 8) * 8). Then primitives like convolutions might work with a rounded-up number of channels instead of the original ones and compute the correct result (adding zeros does not change the result).
That enables supporting an arbitrary number of channels with almost no changes to the kernels. The price would be some extra computations on those zeros, but either this is negligible or the performance with overheads is still higher than the performance with the plain data layout.
The picture below depicts the idea. Note that some extra computations occur during computation of d0, but that does not affect the result.
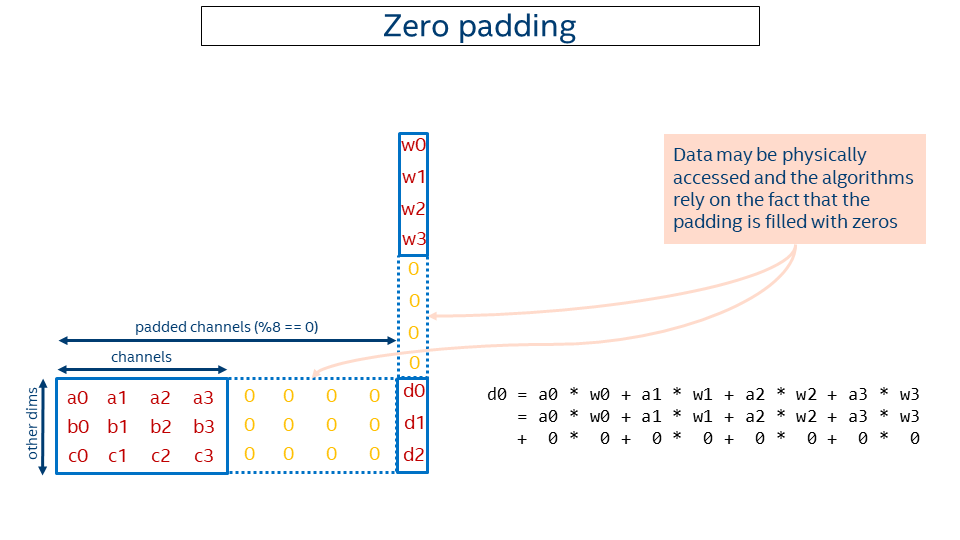
Some pitfalls of the given approach:
The memory size required to keep the data cannot be computed by the formula
sizeof(data_type) * N * C * H * Wanymore. The actual size should always be queried via dnnl_memory_desc_get_size() in C and dnnl::memory::desc::get_size() in C++.The actual zero-padding of oneDNN memory objects happen inside the primitive execution functions in order to minimize its performance impact. The current convention is that a primitive execution can assume its inputs are properly zero padded, and should guarantee its outputs are properly zero padded. If a user implements custom kernels on oneDNN blocked memory objects, then they should respect this convention. In particular, element-wise operations that are implemented in the user’s code and directly operate on oneDNN blocked layout like this:
for (int e = 0; e < phys_size; ++e) x[e] = eltwise_op(x[e])
are not safe if the data is padded with zeros and
eltwise_op(0) != 0.
Relevant oneDNN code:
const int C = 17; const int C_padded = div_up(17, 8) * 8; // 24 // logical description, layout independent const int ndims = 4; // # of dimensions dnnl_dims_t dims = {N, C, H, W}; // dimensions themselves memory_desc_t md; // initialize memory descriptor dnnl_memory_desc_init(&md, ndims, dims, dnnl_f32, // single precision data type dnnl_nChw8c // blocked layout ); ptrdiff_t expect_stride_n = C_padded*H*W; // note C_padded here, not C ptrdiff_t expect_stride_C = H*W*8; ptrdiff_t expect_stride_h = W*8; ptrdiff_t expect_stride_w = 8; ptrdiff_t expect_stride_8c = 1; bool expect_true = true && true // logical dims stay as is && md.dims[0] == N && md.dims[1] == C && md.dims[2] == H && md.dims[3] == W && true // padded dims are rounded accordingly && md.padded_dims[0] == N && md.padded_dims[1] == C_padded && md.padded_dims[2] == H && md.padded_dims[3] == W && true // strides between blocks correspond to the physical layout && md.format_desc.blocking.strides[0] == expect_stride_n && md.format_desc.blocking.strides[1] == expect_stride_C && md.format_desc.blocking.strides[2] == expect_stride_h && md.format_desc.blocking.strides[3] == expect_stride_w && true // inner-most blocking && md.format_desc.blocking.inner_nblks == 1 // only 1 dim is blocked (c) && md.format_desc.blocking.inner_idxs[0] == 1 // 1st (c) dim is blocked && md.format_desc.blocking.inner_dims[0] == 8; // the block size is 8 assert(expect_true);